Do Bigger Tires Affect Speed, Odometer and Gear Ratio?

Bigger tires do impact the speedometer and odometer readings. This happens because their increased diameter makes them rotate slower than the factory tires. So even though the actual speed is the same, speedometers set for the original tires will show slower speeds with the bigger tires. In the same way, since more ground is covered per rotation with the bigger tires, the odometer records shorter distances traveled. So when putting on larger tires, recalibrating the speedometer and odometer becomes necessary. This accounts for their slower rotation over the same distance driven.

Upgrading to bigger tires can leave you scratching your head on how it affects your speedometer, odometer, and gear ratio.

Many factors are at play that impact your vehicle’s performance and reading accuracy when going to a larger tire.

In this guide, we’ll break down in simple terms how tire size influences these components, so you can make an informed decision on the best setup for your needs. The goal is to simplify the science behind the numbers so you know what to expect before hitting the road on new wheels and rubber.

If you have confusion of whether installing big tires affect mpg, you can read my guide on that topic.

My Personal Experience With Bigger Tires and Their Affect On Speedometer

My sister recently got new larger all-terrain tires installed on her 2018 Nissan Titan. Afterwards, she noticed the speedometer reading lower speeds than her actual speed on the highway. The odometer mileage was also less than it should be for the distances driven.

Using a Hypertech speedometer tool, I figured the Titan’s engine control module to properly interpret the wheel speed sensor inputs based on the bigger tire diameter. Recalibrating the ECU computer ensured accurate speedometer and odometer readings with the upgraded tires, avoiding safety problems.

Some Importance Dimensions Of a Tire

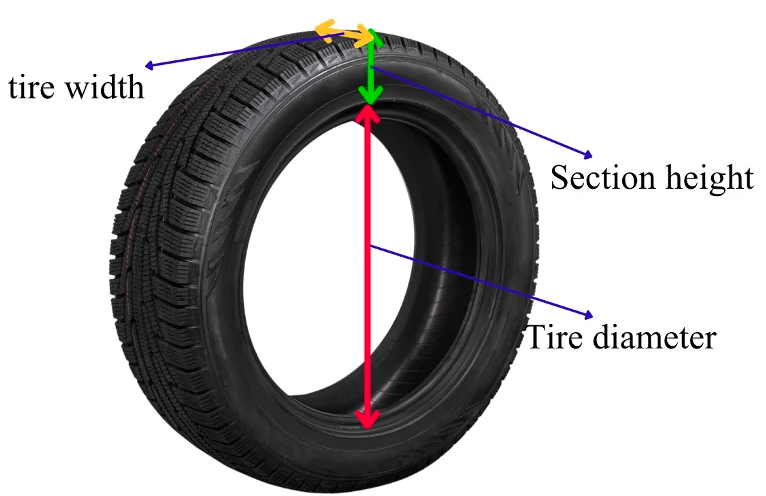
The size of a tire is usually found on the sidewall of the tire and is represented by a combination of numbers and letters.

For example, 175/65R15 84H. The numbers that follow represent the width of the tire in millimeters (175), the aspect ratio of the tire (65), which is the ratio of the height of the sidewall to the width of the tire, and the diameter of the wheel in inches (15). The wheel diameter is the same as the inner diameter of the tire.

If tire width is increased, the section height of a tire should also increase to maintain the same aspect ratio.

You can use this tool to play with the different dimensions of the tire and their effect on the tire revolutions.

The load index and speed rating of a tire indicate the maximum weight and speed that the tire can handle safely. These dimensions are critical to your car’s safety and performance.

Overloading a tire or driving at speeds higher than its rating can increase the risk of a blowout or other serious accidents. In the above picture ‘84‘ is the load rating and ‘H‘ is the speed rating. You can consult this load and speed rating chart to learn more.

Understanding Of Tire Circumference and Its Affect On Speedometer

Tire circumference is the total distance of one revolution of a tire. The circumference of a tire can be calculated using the formula:

C = 2πr

where C is the circumference, π (pi) is a mathematical constant approximately equal to 3.14, and r is the radius of the tire.

Now, many people confuse tire radius with wheel radius. In the above formula of the circumference of the tire, the radius ‘r’ refers to the outer radius of the tire.

The radius of a tire is the distance from the center of the wheel to the outer edge of the tire.

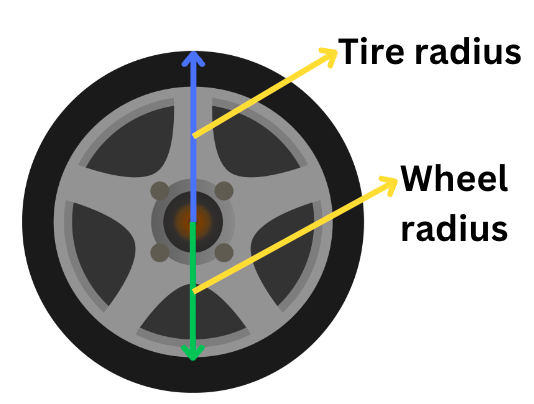
The tire radius is mathematically calculated as follows:

r = wheel radius + section height

In the example at the start of this article, ‘15 in‘ was the wheel diameter. So, its radius will be half i.e. 7.5 inches. 

Aspect Ratio of the tire/100 = Section height/Width of the tire

Since AR of the tire was 65 in the above example and the width was 175mm, section height = 65/100 x 175 = 113.75 mm =  4.4783 inches.

Now, tire radius can be calculated as r = wheel radius + section height = 7.5 + 4.4783 =  11.9783 inches.

Now, we can calculate its circumference as follows:

C = 2πr = C = 2 x π x 11.9783 = 75.3989 inches.

This means that for every full rotation of the tire, the vehicle will travel a distance of 75.3989 inches. This is the same as if you cut the tire into a straight piece of rubber, its total length will be equal to its circumference in a circular shape.

Tire circumference is an important factor to consider when changing the size of the tire. As we saw earlier, a larger tire will have a greater circumference than a smaller tire. This can have an impact on the vehicle’s performance, including its acceleration, braking, and handling characteristics.

How Do Bigger Tires Affect Speed Of A Vehicle?

Bigger tires have the same linear speed as smaller tires, but they rotate slower. Linear speed is how fast you’re going down the road. Rotational speed is how fast the tire spins around.

Bigger tires take fewer spins to go the same distance. That’s because they’re bigger around. Think of a really big tire compared to a tiny tire on a tricycle. The big tire doesn’t have to spin as much to go far.

Same with your vehicle. Putting on bigger tires keeps your vehicle going the same speed. But the tires spin slower since they’re bigger around. Each turn of the big tire takes you farther than a small tire.

So bigger tires decrease the spins per minute. But your truck or car still goes the same miles per hour. Big tires rotate slower but cover more ground per turn.

We can demonstrate this relationship using a simple formula where the linear speed (V) of a vehicle is equal to the tire’s rotational speed (R) multiplied by the outer radius of the tire. 

V = R x C/2π

If we assume a vehicle is traveling at a linear speed of 60 mph (miles per hour) with tires that have a circumference of 75.3989 (calculated in the previous section), the tire’s rotational speed would be:

R = V / C  = 60 mph x 2π/ 75.3989 inches ​≈ 840 RPM.

Note: Here, I have not completely shared the calculations as the blog post will be more complex. Being an engineer, I want to just keep things simple. So, I thought I shouldn’t show calculations. In the background, I converted them into the same units i.e. inches to miles. Then, I converted the final result, which was in radians/hour into RPM. 

Now, if we increase the tire size to one with a radius of 14 inches, its circumference will be 87.92 inches. The vehicle’s linear speed will still be 60 mph but the rotational speed of the tire will decrease.

R = V / C  = 60 mph x2π/ 87.92 inches ≈ 720 RPM

After that, the control unit processes the speed of the tires (RPM) to calculate the vehicle speed in mph, which moves the needle to display the vehicle speed.

Technically, linear speed i.e. vehicle speed remains the same with both original factory tires and bigger tires. This speed doesn’t depend on the size of the tires.

However, the control unit in vehicles processes RPM into linear speed by taking into account the tire size. Since, the tire size given as the input by the manufacturer is the factory tire size, the linear speed will be displayed less.

So, if the wheel speed determined was 720 RPM, and the control unit of the vehicle considered the previous tire size i.e. 11.9783 inches (75.39 inches of circumference), the linear speed shown by the speedometer of your vehicle will be 51.306 mph. 

How Do Bigger Tires Affect Odometer?

The circumference of tires impacts the odometer readings. With every rotation, bigger tires cover extra ground distance. But the odometer calculates linear distance from angular rotation. So the odometer will show fewer miles than the actual driven distance.

To find the tire size impact on odometer readings, compare old and new tire circumferences. Calculate the ratio of old tire circumference to new tire circumference. Then multiply this ratio by the distance covered with original tires. This gives the real distance driven.

Angular distance of a new tire = (Old tire circumference / New tire circumference) x Angular distance of an old tire

Just like the angular speed and linear speed discussed in the previous section, a tire (or any circular shape) has an angular distance (θ) and a linear distance (S).

To explain the angular distance for you, I have created an illustration below:

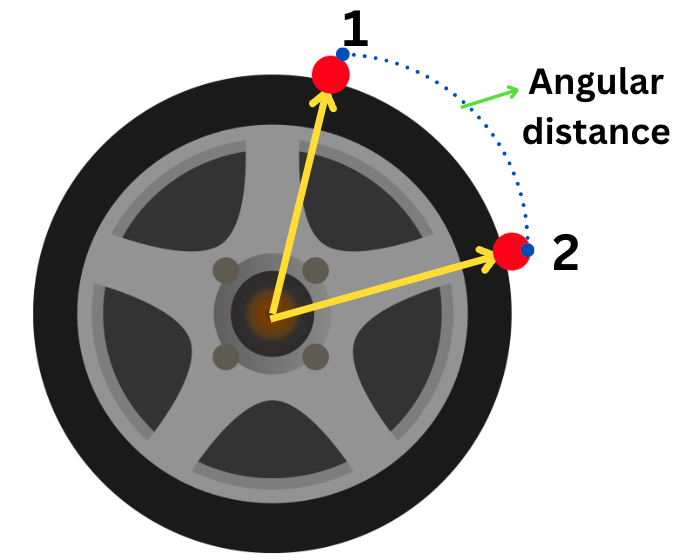
In the above picture, you can see that after some time, the point on a tire (red dot) moves from position 1 to position 2. That distance along the circumference of the circular shape of the tire is called angular distance. It is expressed in terms of the ‘radians’ unit.

Now, let’s say your tire has a radius (r) of 12 inches and it has to cover a linear distance (S) of 3 miles.

The mathematical relation between angular distance and linear distance is as follows:

θ = S/r

To make a calculation, ‘S’ and ‘r’ should be in the same units. So, convert 12 inches to miles, which becomes 0.000189394 miles.

θ = 3/0.000189394 = 15,844 radians ≈ 2521 revolutions.

So, the above result shows that a tire with a radius of 14 inches will have to rotate 2521 times to cover a distance of 3 miles.

In the previous sections, I calculated the circumferences of 12 inches and 14 inches tire sizes as 75.39 inches and 87.92 inches respectively.

So, the angular distance by a 14 inches tire to cover the same linear distance of 3 miles is:

θ = 75.39/87.92 x 2521 = 2161 revolutions. 

Now, 

Assuming the old tires have a radius of r1 and the new, bigger tires have a radius of r2, the angular distance covered by the old tires is calculated as:

θ1 = s / r1

And the angular distance covered by the new, bigger tires is calculated as:

θ2 = s / r2

The impact on odometer reading due to a bigger tire will be a percentage difference between θ1 and θ2 can be calculated using the following formula:

% impact on odometer reading = (θ2 – θ1) / θ1 x 100 = (2161-2521)/2521 x 100 = 14.28%.

This means that the odometer reading with the new, larger tires would be 14.28% lower than the actual distance traveled.

Just like linear speed, technically, a vehicle covers the same linear distance as well. 

But since the engine controller has an input of old tire size, it will not process the correct linear distance and shows a lesser linear distance than the correct linear distance covered by the vehicle.

How Do Bigger Tires Affect Gear Ratio?

The overall wheel diameter grows when larger tires are installed on a vehicle. This happens because the combined wheel and tire size becomes bigger. With every turn, the wheel covers more ground. So the vehicle travels farther with each tire rotation.

Gear ratios affect how power gets to the wheels. The ratio depends on the number of teeth meshing on two gears. It decides how many times the input shaft must rotate for one output shaft turn. High gear ratios can make acceleration sluggish. Fuel efficiency may also drop.

Here, the gear ratio is basically the axle ratio. It refers to the ratio between the number of revolutions of the driveshaft and the rear axle. This is how a vehicle axle looks:

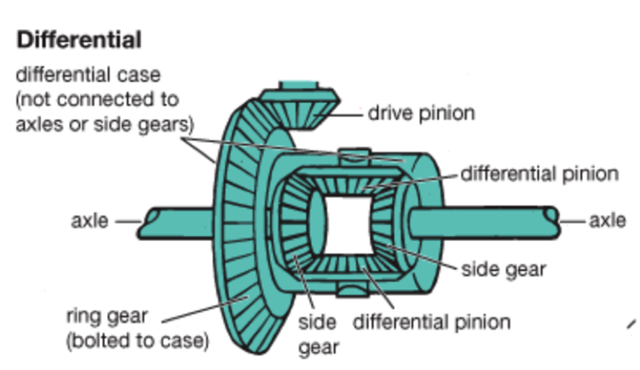
The drive shaft of the transmission has a pinion gear that transfers the power to the ring gear. From the ring gear, power is transferred to the side gears, which rotate the tires of the vehicle. 

Once the tire size is changed, the effective gear ratio also changes as the tire is also acting as a gear.

To understand this better, let’s consider two different scenarios. In the first scenario, we have a vehicle with a stock tire radius of 12 inches and a gear ratio of 3.73. In the second scenario, we upgrade to a tire radius of 14 inches. 

To calculate the new gear ratio, we can use the following formula:

New Gear Ratio = (Old Gear Ratio x Old Tire Diameter) / New Tire Diameter

Using this formula, we can calculate the new gear ratio as follows: New Gear Ratio = (3.73 x 12) / 14 = 3.197

From this calculation, we can see that the gear ratio has effectively changed from 3.73 to 3.197. This means the engine will have to work harder to turn the larger tires, resulting in a loss of torque and acceleration. Due to this reason, fuel consumption also increases when you shift to bigger tires.

FAQs